Colour

Humans perceive colour through three kinds of cone cells that sense light (electromagnetic radiation) of different frequencies.

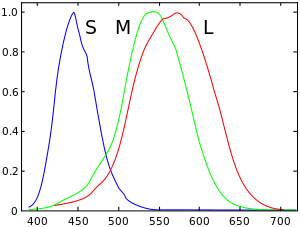
These cone cells have peaks of spectral sensitivity in short (S, 420nm - 440nm), middle (M, 530nm - 540nm), and long (L, 560nm - 580nm) wavelengths.

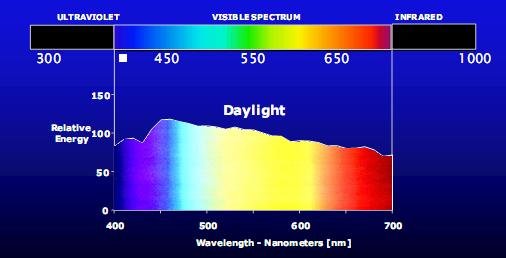
What we perceive as colour is a result of different light frequencies activating our three cone cells by different amounts. Hence, we can associate every distribution of light frequencies with a certain colour. This distribution of frequencies is known as a spectral power distribution (SPD). For example, the below diagram shows the SPD of daylight [2]. The combination of the relative amounts of these frequencies activating our cone cells produces the perceived colour of daylight.

Given an SPD, we can convert it into sRGB, a widely used colour space for displays. This process is twofold. First, we convert the SPD into the XYZ colour space. Then the XYZ colour is normalized with respect to a whitepoint (in this example we use the D65 whitepoint), and converted to sRGB.

The XYZ colour space is described by three values $X,Y,Z$. The colour matching functions $\bar{x}(\lambda),\bar{y}(\lambda),\bar{z}(\lambda)$ describe the relative amounts that a given wavelength contributes to the values $X,Y,Z$ respectively.

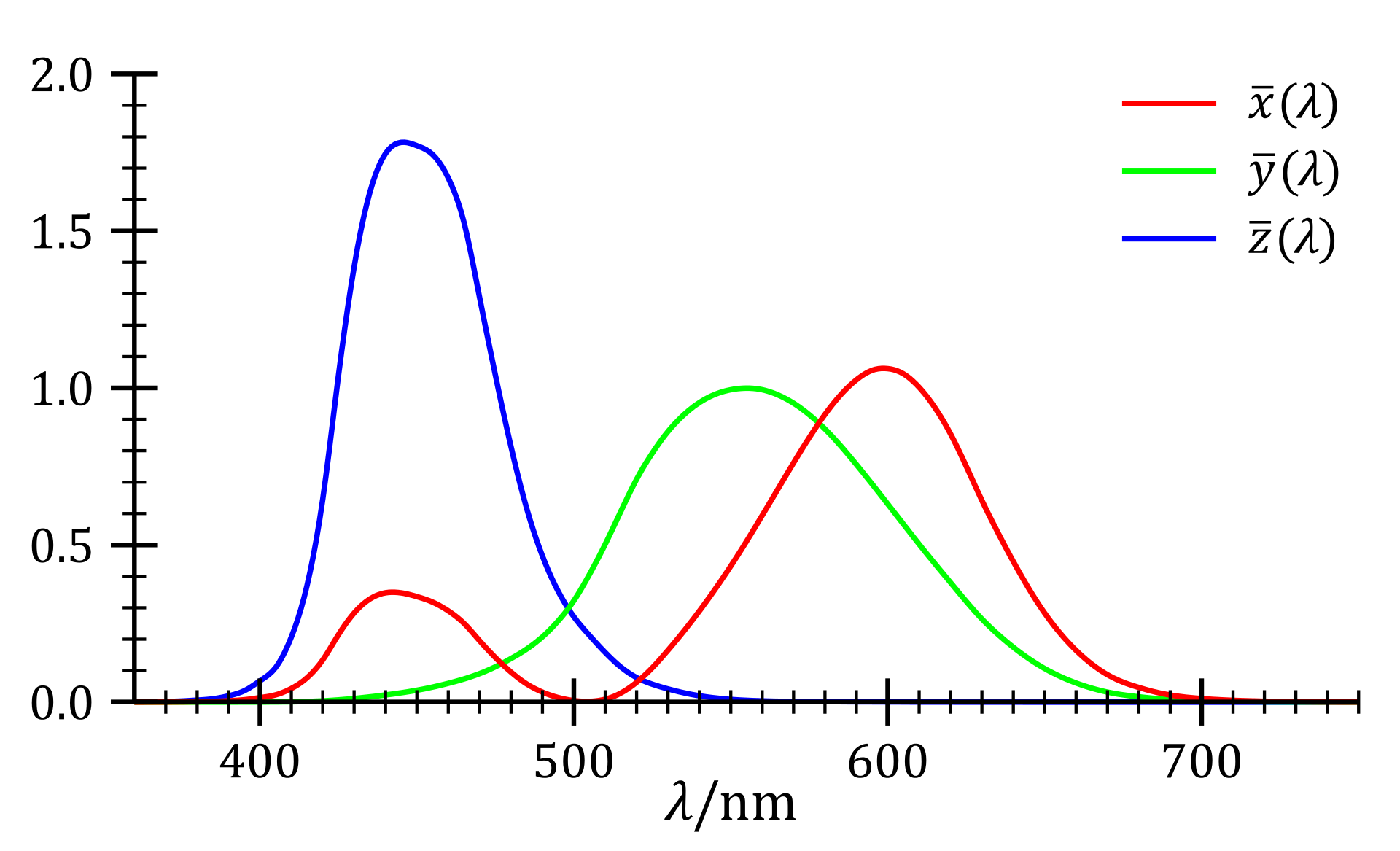
Hence, given an SPD $I(\lambda)$, we can find the $X$ value by multiplying $I(\lambda)$ with the colour matching function $\bar{x}(\lambda)$, then integrate the resulting function. Explicitly,

\[X=\int_{380}^{780}\bar{x}(\lambda)I(\lambda)d\lambda\]

Similarly, for $Y$ and $Z$ we have:

\[\begin{align*} Y&=\int_{380}^{780}\bar{y}(\lambda)I(\lambda)d\lambda\\ Z&=\int_{380}^{780}\bar{z}(\lambda)I(\lambda)d\lambda \end{align*}\]

In terms of implementation detail, we approximate the integration via a discrete sum. The colour matching functions $\bar{x}(\lambda),\bar{y}(\lambda),\bar{z}(\lambda)$ can be approximated using sums of piecewise Gaussian functions, given by [1].

We now normalize $X,Y,Z$ with respect to the D65 whitepoint. From the SPD $I_0(\lambda)$ of the D65 whitepoint, we can calculate its $X,Y,Z$ values, which we denote here by $X_0,Y_0,Z_0$.

The normalized values of $X,Y,Z$ with respect to the D65 whitepoint are then given by:

\[\begin{align*} X_{D65}&:=\frac{X}{Y_0}\\ Y_{D65}&:=\frac{Y}{Y_0}\\ Z_{D65}&:=\frac{Z}{Y_0} \end{align*}\]

This process normalizes the $X,Y,Z$ values such that the normalized $Y$ value (which represents luminance) of the D65 whitepoint is 1.

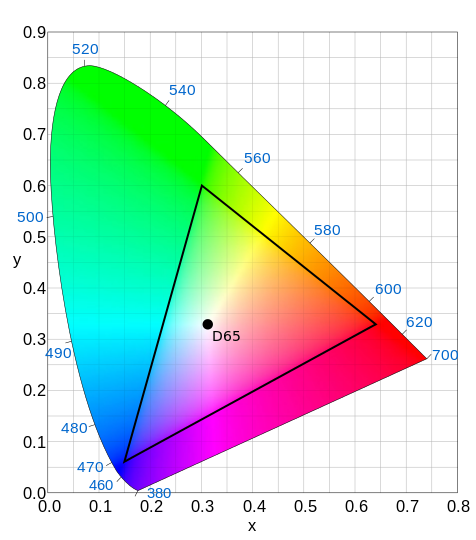
Furthermore, the chromaticity values $(x,y)$ (see below) are unchanged.

Next, we convert the normalized XYZ values into sRGB:

\[\begin{bmatrix} R_{\text{linear}}\\G_{\text{linear}}\\B_{\text{linear}} \end{bmatrix}=\begin{bmatrix} 3.24096994 &-1.53738318 &-0.49861076\\ -0.96924364&1.8759675&0.04155506\\ 0.05563008&0.20397696&1.05697151 \end{bmatrix}\begin{bmatrix} X_{D65}\\Y_{D65}\\Z_{D65} \end{bmatrix}\]

Finally, gamma correction must be applied to these values:

\[\begin{bmatrix} R\\G\\B \end{bmatrix}=\begin{bmatrix} \gamma(R_{\text{linear}})\\\gamma(G_{\text{linear}})\\\gamma(B_{\text{linear}}) \end{bmatrix}\]

where

\[\gamma(u):=\begin{cases} 12.92u&u\leq 0.0031308\\ 1.055u^{1/2.4}-0.055&\text{otherwise} \end{cases}\]

Converting XYZ to xyY

Additionally, we can also convert the XYZ colour value into the xyY colour space which is defined as:

\[\begin{align*} x:=\frac{X}{X+Y+Z}\\ y:=\frac{Y}{X+Y+Z} \end{align*}\]

and $Y$ referring to the same quantity in both colour spaces.

The $(x,y)$ values denote chromaticity (see diagram below) and $Y$ is a measure of luminance (brightness).

Interactive SPD to sRGB Converter

For best colour accuracy, you should view this on an sRGB monitor.